塾長のひとりごと
初心者のための埼玉県公立入試4
ところで学習記録の評定が1年から必要だということをお話しました。
1・2・3年の評定は各45点満点です。
そのまま合計すれば135点満点ですが、そのまま合計した数字が点数ではありません。
高校によって学年ごとにウェイトをかけることができるのです。
直近の中学3年の成績を重視するならば1年:2年:3年=1:1:3となることが多いです。
この場合45+45+135=225点満点となり3年が1,2年の3倍の扱いになります。
1年、2年、3年を同等に扱うのならば1年:2年:3年=1:1:1となります。
この場合は45+45+45=135点満点になります。
他にも1:1:2や2:2:3などのような中間型もあります。
一昔前の調査書(相関法式のころ)では中3を中心にして中1、2を加味するというものでした。当時、比率などは公表されていませんが、今の比率でいうと1:1:8などと言われていました。
そこまでではなくとも、中3より中1、中2が重視されることはないので中3がより大切になります。
また、この比率は毎年変更が可能になっています。
中1:中2:中3の比率は受験をする中3の7月にならないとわかりません。
現在中1、中2の生徒は今からしっかり意識をして、どちらに転んでもいいという状況にしておいたほうが良いということになります。
中学1年生は初めての中間テストを受けるところだと思います。今回の結果も受験に関係するということになるのでしっかり対策をしましょう。
2016年05月24日
初心者のための埼玉県公立入試3
今回から調査書についてもう少し詳しく見ていきます。
埼玉県公立28年度入試調査書はこちら
学習の記録
学習の記録は評定と言われるものでその点数は保護者・生徒も知ることができるものです。3学期に渡される通知表の4列目(2期制ならば3列目)の数字がその学年の評定となります。
評定は通知表の1学期~3学期(前期・後期)の平均で付けられることがほとんどです。
平均で付けられるということは次の場合はどうでしょう。
1学期3 2学期3 3学期4
(3+3+4)÷3=3.3333… となりますのでほとんどの場合3となりますが、必ずしも3とは限りません。
この場合4になることもあります。同じ3でも4に近い3か、2に近い3かで変わってきます。3が2回続いたからもう4は無理だと思わずに、最後まであきらめずに頑張りましょう。
また、3だからと安心していると3,3,2で2ということもあり得るということです。通知表では3は安心できる数字ではないということです。また今の通知表は絶対評価で付けられるものなので3は真ん中ではないということも言えます。
定期テストではどうしても主要5教科(英数国理社)に目が向きます。しかし、評定は9教科であるということを1年の最初から意識しておいたほうが良いでしょう。後になってあの時もっとやっておけばとならないために提出物・授業態度にも気を付けたいところです。成績というと主要5教科にとらわれがちですが実技であっても5は5です。実技が得意という人は稼げるところでしっかり稼いでおきましょう。
「公立入試は入学してからすでに始まっている」ですね。
2016年05月23日
初心者のための埼玉県公立入試2
得点の付け方
学力検査の点数は500点満点(英数国理社 各100点満点)。ただし、傾斜配点を除く。
そして内申点は高校ごとに満点が異なります。そして内申点の満点を調節することで学力検査の点数重視か内申点重視かが決まってきます。偏差値の高い学校ほど学力重視の傾向が強くなりますがどのレベルであっても内申点が無くて良いとはなりませんのでしっかりと中学校の勉強及び活動にしっかり力を入れましょう。
それでは、内申点とはどのように決まるのかを見ていきましょう。内申書は入学願書とともに提出されるもので書くのは中学校の先生です。それを受け取った側の高校で点数化します。次の3つの項目に学校ごとに満点を決めてあり、例年7月にその年の選抜基準が発表されます。29年度入試の選抜基準はあと2ヶ月ほどしないとわからないということになります。
・学習の記録 9科の5段階評価(通知表)学年ごと
・特別活動などの記録 生徒会活動 学級活動 部活動など
・その他の項目 検定 資格 総合的な学習の時間の記録など
内申書はこちら
この3つの合計点×係数が内申点と呼ばれるものです。係数によって最終的に満点が決まる。
次回はその3つの項目を細かく見ていきましょう。
2016年05月20日
初心者のための埼玉県公立入試1
年度の呼び方
入試では●年度入試という呼び方がよくされます。
今は平成28年なので、現中3生が受ける入試が29年度入試となります。
29年度入試とは来年の3月に入試を受けるので29年度入試と覚えていれば問題ありません。
本来は、29年度の高校1年生を選抜する入試が29年度入試となります。
ちなみにですが「平成29年度埼玉県公立高等学校入学者選抜」というのが正式な名称です。(以下29年度入試)
教育委員会のホームページなどを見る機会がある人は覚えておいたほうがいいでしょう。
29年度入試から学力検査に変更がありますがそれはまたの機会で取り上げます。
公立入試の選抜方法
私立高校は日程さえクリアできれば何校でも受けることができます。そして私立では事前相談がほぼ合否を決めるということになっています。
では、埼玉県公立高校は何校受けられるでしょうか?
答えは1校です。(国立をうけると最大2校です。)県立高校は1校しか受けられず、チャンスは1度です。以前推薦入試があったころは2回チャンスがありましたが、今となってはどちらが良いのかわかりませんが…。
選抜方法についても相関方式から加算方式へと変わりました。ここでは相関方式の説明は省略し、現在行われている加算方式について説明していきます。加算(足し算)ですので文字通り足し算の合計で合否が決まります。当然合計が大きい人から受かっていくというものなのですが、何と何の足し算なのでしょうか。
(内申点)+(学力検査の点数)で合否が決定します。
2016年05月19日
号外 定期テスト対策数学
1学期中間テスト数学の注意点
中1 正負の数の意味 正負の数の計算
おそらくこの辺りが多いと思います。場合によっては小学生の復習が入ることもその場合は学校のワークに該当ページが載っていることが多いので活用しましょう。
正負の数の計算がどこまで行くのかは学校ごと、先生ごとに差が大きいですが100点を目指しているのなら必ず用語をチェックしてください。正の数、負の数、自然数、加法、減法、絶対値、原点など教科書に説明が載っている場合は教科書でチェックをする。加法の交換法則、加法の結合法則なども意味(2つの違いを確認)と言葉をしっかり覚えておきましょう。「項」の様に聞きなれない言葉もしっかり覚えましょう。
中2 式の計算
1年の『資料の活用』が範囲になっている場合は要注意。特に2年になってから授業で扱わず。1年3学期の期末テストで出せなかったために今回の1学期中間テストに入っているときは要注意。忘れてしまっている可能性が高いので早めに手を付けましょう。式の計算は1年の文字式の計算ができていればさほど問題は会いません。ここでつまずくようだと1年の文字式の計算からやり直したほうがいいです。1年と同様に言葉のチェックを怠らずにしっかり覚えましょう。計算以外にも次数や係数など理解ができていないと思わぬところで点数を落としてしまうので注意。
中3 式の展開・因数分解
2年の『確率』が範囲になっている場合は要注意。特に確率は入試においても重要になってきますので範囲になっていれば力を入れてやっておくべき単元です。
文字式の計算の一つですが公式を暗記して当てはめるという考え方は計算においては初めて出てくる考え方です。考え方を変えてそれに慣れないといけないということです。注意が必要なのは展開を公式でしっかり暗記していないと因数分解ができなくなります。非常手段として展開までしか範囲がない場合は公式を使わず、分配法則だけで答えを出すことはできますがお勧めはしません。
今回のテスト範囲では計算もさることながら用語のチェックと場合によっては前学年の復習単元がカギを握ることになるかもしれません。
中1・中2・中3ともにこの1学期の最初の単元はその後の単元につながっていく大事な単元です。テスト対策(事前対策)も大切ですが、テスト直し(事後対策)も大切です。
面談 入塾面談・体験 24時間受付中 クリック
2016年05月19日
実は算数で大切なもの(続き)
前回の続きです。
例えば、小数の足し算で4.8+7=という問題。このとき8に7を足して5.5としてしまうようケースが見られます。
間違いを指摘するときに小数の足し算では小数点をそろえるんだよね、と教えますよね。
それはもちろん間違っていませんが、まずは位取りがしっかりできているのか、意味も理解しているかどうかを認識させることが大事なのです。
この確認をしっかりしないと、指摘されたらそうだったと言って直して解けるのですが、何度も同じ事を繰り返すことになります。間違いを直すとは次に出てきたときに間違わずにできるかが重要なのです。
一番いいのは最初に位取りが出てきたときから位取りを理解する学習ができていればいいのです。
どんなにけた数が大きくなっても同じことだと気づけるとあとは勝手に理解していきます。
さらには一の位より小さい位がある(小数)ことを理解させていけばスムーズに小数の学習に入ることができるので躓かずに済みます。
また概算(およその数の計算)については概算の問題が解けたらこの単元は終わりとなってしまいがちです。しかし、それだけではないその先にあるこの単元を習うことの意味を理解できていれば活用できる大事な単元なのです。残念ながらできる子でも活用できているケースはあまり見られません。
どういうことかというと計算問題ではまず最初に概算をしておくということです。この癖(習慣)がついていることで、つまらないミスに気が付くことができます。例えば先ほどの4.8+7も概算しておけばおよそ5+7=12となるので、本当の答えはそれよりちょっと小さいということが概算できていれば5.5という答えが出た時点で「あれ」おかしいなと気づけるのです。概算を習う前からそういう習慣(考え方)を身に付けさせるといろいろな場面で『気づく』ということに気づくようになります。文章問題で、とんでもない答えをそのままにしてしまうケースも概算(答えの見込み)を意識していない表れです。すぐに身につくことではありませんが強力な武器であることは間違いありません。
2016年05月18日
取材を受けました
2016年05月17日
実は算数で大切なもの
皆さんは小学校の算数で大切なものと言われて思いつくものは何ですか。
割合・速さ 確かに重要です。
分数・小数 計算はすべての基本ですので確かに重要です。
図形の問題 中学でも同じ単元が出てくるので重要ですね。
他にもいろいろな考え方があると思います。
もちろん上に上げたこと、さらに言えば全ての単元が必要だから学習しているわけですが。
算数の単元の中で上に上げたことは重要と思っていると方も多く、それはそれで間違ではありません。
しかし、今日お話しするところは算数で重要だけど意外と見過ごされている単元のお話です。算数が得意になって欲しい。中学受験を考えている。そんな人は是非最後まで読んでください。
ここでは2つ挙げておきます。1つ目は位取りです。えっ…何で位取りと思った人もいるともいます。わかっている人も多いので意外に思うかもしれません。この単元は他の単元の様にそれが理解できていないことが分かりづらい単元だからこそ要注意なのです。
そしてもう1つはおよその数、概算です。どちらもそれほど時間をかけてやることがないので出来ていないことが見過ごされてしまいがちです。
そしてこの2つの単元は単元テストで100点を取ったらそれで全てOKということではないということです。問題が解けることと理解することは違うのです。
続きは次回
2016年05月16日
初心者のための埼玉県私立入試 6
個別相談について基準の見方をお伝えしてきましたがいくつかの注意点があります。
通知表の基準や偏差値の基準に成績が達していても相談結果が?になってしまうことがあります。
それは
通知表の1は不可
欠席日数●日以内であること
というものです。
欠席日数は学校ごとに見る期間が3年次や3年間など違います。多いのは年10日、厳しい学校は年5日というところもあります。
これはどちらも入学後に問題ありという判断をされてしまうということです。欠席日数が気になる場合は学校ごとに確認をしてください。
通知表や北辰偏差値に加点をするということもあります。
学校ごとに色々な加点ポイントがあります。例としてあげると以下のようなものがあります。
生徒会など 委員会など 部長など 部活動の実績 コンクール ボランティア 各種検定など 皆勤 精勤 兄弟や親の在校・卒業
学校ごとにどの項目で何ポイント貰えるのかは実際の相談で確認してください。上の例以外にもやる気ポイントを設けているところなどもあります。
やる気ポイントとは説明会参加などのその高校への意気込みポイントと言えば良いでしょうか。
いずれにしても相談ですから行きたいという意気込みが伝わると高校の先生も足りない分をポイントで探してくれるということもあります。ぜひ積極的に相談してください。
また、公立第一希望なので私立はどこでもという考え方はあまり賛成できません。何故ならば、公立入試前に私立入試が終わり40日ほど期間があります。このとき、どこの私立に受かっているのかで気持ちの持ち方が違ってくるということがあるからです。私立選びに関しても精いっぱいやったということが迷いを生まないために大切なのです。
2016年05月14日
初心者のための埼玉県私立入試 5
>受験情報
前回に引き続き基準を見るうえでの注意点の話です。
どの私立も通知表の基準と偏差値の基準を示しているのが普通です。
このとき、2通り見方がありますので注意が必要です。
それが前回予告していたandかorの違いです。
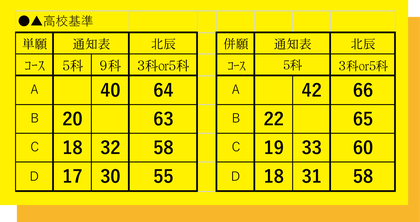
通知表の基準で5科と9科の基準が出ているときはorです。つまりどちらか一方の基準で照らし合わせるということです。同様に北辰テストの偏差値で3科と5科の基準が出されている場合もorです。問題なのは通知表の基準と偏差値の基準が
and なのか or なのかということです。
andの場合
通知表と偏差値の両方の基準を満たしていなければいけないということです。
例えば表の単願Cコースがandの場合
通知表5科18 and 偏差値58
または 通知表9科32 and 偏差値58
orの場合
通知表か偏差値のどちらか一方の一つの基準でクリアしていればいいということになります。
ところorの場合、通知表の基準と北辰テストの偏差値の基準を比べるとどちらをクリアしているほうが良いのか?
面談を担当する先生にもよりますが、偏差値の方が客観的な学力を見ることができるので偏差値でクリアしているほうが良いと考える先生もいます。この場合は入学してからの学力を心配してのことです。
また、通知表が良いということは学習習慣(学校の言うことをしっかり守れる。)がついているから入学してから伸ばしていけばいいと考える先生もいます。
つまり結論は合格のしやすさはどちらでも同じと言えます。
合格した後のことまで考えると
通知表でクリアしていても偏差値でクリアしている場合のでも、偏りがある場合は自分の弱点を知ることでその後の学習の指針にするといいと思います。入学して終わりではないですから単願の場合は特に注意が必要です。相談でいい結果をもらえても油断は禁物です。
2016年05月09日
初心者のための埼玉県内私立入試3
今回は事前相談についてもう少し細かく見ていきましょう。
学校説明会などにより相談の基準が各高校から出されます。学校ごとに様々な基準が用いられますが大きなものでは次の①②の2つがあります。
①中3の1学期または2学期の通知表
②原則2学期以降の北辰テストの偏差値
③その他
まずは①の通知表について
中3の通知表の3科や5科や9科の合計で基準が示されます。
5科であれば25点満点、9科であれば45点満点となります 。
何科目の合計かは学校ごとに決められるものなので学校やコースごとに確認が必要です。
5科(英数国理社)または9科(実技科目もすべて)で示されることが多いですが、中には3科(英数国)や変則な科目の場合もあります。
いずれにしても学校ごとに色々な基準がありますので確認が必要です。
1学期または2学期となっていますので1学期に基準をクリアしていることが望ましいです。
1学期で基準をクリアしていれば仮に2学期に成績が下がったとしても1学期の通知表コピーを見せて相談するので問題ありません。
1学期でクリアしておくことが望ましい理由ですが、1学期の通知表でOKが出ないということは2学期の通知表が出てから12月の最終相談で私立高校に持っていくことになります。
そうなるとそれまで通知表による相談ができないということになります。例えばA校に相談したら「2学期の通知表で5科の合計で20になったら持ってきてください。」というふうに言われた場合ダメならB校というように2段構えか必要になってくるからです 。併願の場合、県立もそれによって変わる場合などは影響が出ますので要注意です。
ポジティブに考えれば2学期通知表待ちで、よりレベルの高い県内私立を滑り止めに考えることもできるということですが… 。とはいえ早めに私立高校を決めて本命の県立に向けて頑張らなければいけないことを考えると1学期の通知表でOKを貰っておいたほうが良いと言えます。私立単願(第一志望)ならなおのことです。
今は通知表のことだけで話をしましたので実際には北辰テストの結果も絡んでくるので次回はその話からしたいと思います。ただ、北辰が駄目でも通知表で救われるケースが多く見られるのも事実です。
2016年05月05日
初心者のための埼玉県私立高校入試 2
前回は埼玉県の私立高校入試はほぼすべての生徒が推薦入試を受けることになるというお話をしました。
今回は埼玉県私立入試に欠かせない制度について説明していきます。
それは個別相談(事前相談)という制度です。(一部の難関付属を除く)
かなり昔に遡りますが、以前埼玉県の私立入試では偏差値輪切りということが行われていました。中学校の先生と高校の先生の間で相談をしていました。そこでは、確約という言葉も…、その後いろいろあって今の形になったのです。いろいろの部分は話が長くなるので別の機会で。
話を戻しまして、個別相談とは何かというと、保護者・生徒と私立高校の先生の間で事前に合格の可能性について相談を行う制度のことです。
相談時期は2学期の10月~12月に高校の説明会と同時開催でれることが多いようです。中には事前に予約を取らないといけない学校や面談の日を別に設けるケースもあります。
では、何をもって合格の可能性を相談するのかですが、それは中学校の3年1学期or2学期の通知表と7月(4月)以降の北辰テストの偏差値で相談します。
そしてこの相談なしに受験をすることは可能ですが合格の可能性は極めて低くなります。相談なしに受験をするのは無謀ということになります。
2016年04月28日
割り算でつまずかないために③
今回は割り算を習いたてで文章問題に取り組むときの注意点を上げておきます。
割り算に限らす低学年の文章問題は、答えはわかるが式が言えないという現象がよく見られますが、特に割り算の文章問題ではその傾向が出やすいので気に留めておいたほうが良いと思います
例えば次のような問題で見ていきましょう。
15人の子供が3人ずつのグループに分かれます。いくつのグループができますか。という問題です。
すぐに5つと答えたとしてもここで15÷3=5 と考えているかはわからないということです。
3×□=15だから□に入るのは5だと答えを出しているとします。計算の仕方を考えると確かに割り算は頭の中で上のような九九を思い浮かべて5という解答を導くのですが、15÷3= という式を作らずかけ算で答えが出せている子は要注意です。
例えが2ケタ以上の割り算になると九九では対応できないのでつまずくということがあります。
さらには小数・分数になってくると数字ではなく言葉で式が作れないといけなくなります。
ですから最初のうちは割り算とは何かを学習しているということを考えさせないといけないということです。
3人ずつ分けるから割り算だよねと確認し、割り算の式を書かせることが大切なのです。むしろ文章問題とはこの部分の確認のために解いているということが言えるのです。
2016年04月28日
初心者のための埼玉県の私立高校入試 1
埼玉県の引っ越してきたかたや初めてのお子様が高校入試を埼玉県で受ける方へなるべくわかりやすく説明していきます。よって大筋をおった説明になりますのでご了承ください。
細かいところまで説明しすぎないように気をつけていきますので細かいところが気になる方はお手数ですがお問合せください。
早速ですが埼玉県の私立高校推薦入試は他の都道府県とはかなり異なります。
押さえておかなければいけないポイントは…
埼玉の私立は一部の学校を除いて推薦入試ですべて決まるということです。
推薦入試というと面接というイメージか、テストがあっても簡単なものという形で理解しているのではないでしょうか。そして推薦がだめなら後で一般入試を受けるというのが持たれているイメージだと思います。また、推薦を受けるのは私立第一志望の生徒で、公立(県立)第一志望者は一般入試を受けると考えている方もいると思います。
ところが、埼玉県の場合、一部の学校(慶応志木・早稲田本庄・立教新座)は上記のような制度を利用しますが大半の県内私立高校は推薦入試でほぼ定員が埋まり、一般入試があってもそれは2次募集的な形で少数の募集になっています。私立第一希望者は単願推薦を、公立第一希望者は併願推薦という形でいずれも私立の推薦入試を受けることになります。(少数ですが県立1本という場合もありますが)また、隣接する都内私立では一部埼玉方式を埼玉の中3受験生に適応するということもあります。つまり埼玉県の入試=推薦入試ということが完全に根付いているのです。
2016年04月26日
割り算でつまずかないために②
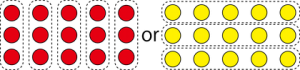 前回の続きですが計算の時は右側の黄色で考えることになります。÷というと5つに分けるというほうが頭に浮かぶかもしれませんが計算では5つずつに分けると考えます 。例えば、÷100という計算を100人で分けるというのが頭に浮かべられるかどうかということです。
前回の続きですが計算の時は右側の黄色で考えることになります。÷というと5つに分けるというほうが頭に浮かぶかもしれませんが計算では5つずつに分けると考えます 。例えば、÷100という計算を100人で分けるというのが頭に浮かべられるかどうかということです。
100人にわけていく画像を思い浮かべ一人いくつになるかは到底考えられません。
1500÷100のとき「100というかたまり」がいくつ入るのかという考え方で計算するということです。
また、筆算で商を立てるときを考えるとわかると思います。
さらに、足し算の概念を教えるとき合わせていくつ、とやるのと同じことを割り算でやると
いくつ入るかを考えさせるということです。
それを探すのに九九で考えるということになります。
この「かたまりが何個入るか」という考え方は、いずれ悩まされることになるかもしれない単位量につながるので油断できないところです。
2016年04月25日
割り算でつまずかないために①
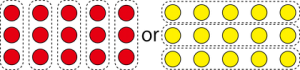
15÷5という式であらわされる問題を2問作りましょう。(ヒント)絵を見てください。
実は15÷5の÷5には2つの意味があります。
1つは15個のものを5つにわけるという意味。
もう一つは15個のものを5つずつに分けるという意味です。
文章問題で式を作る説明をするときは言葉を強調して言ってあげるといいですよ。
15個のキャンディーを5人で分けるとき一人分は何個?
という問題では5つに分けるから15÷5だね。という感じで。
2つの意味があることを知っていることが大事です。
では15÷5の計算をする時は頭の中でどう考えることになるか。
赤か黄色か?どちらで考えているでしょうか。続きは次回です。
2016年04月21日